

As with any recursive formula, the initial term of the sequence must be given.A recursive formula for an arithmetic sequence with common difference.The terms of an arithmetic sequence can be found by beginning with the initial term and adding the common difference repeatedly.The common difference is the number added to any one term of an arithmetic sequence that generates the subsequent term.
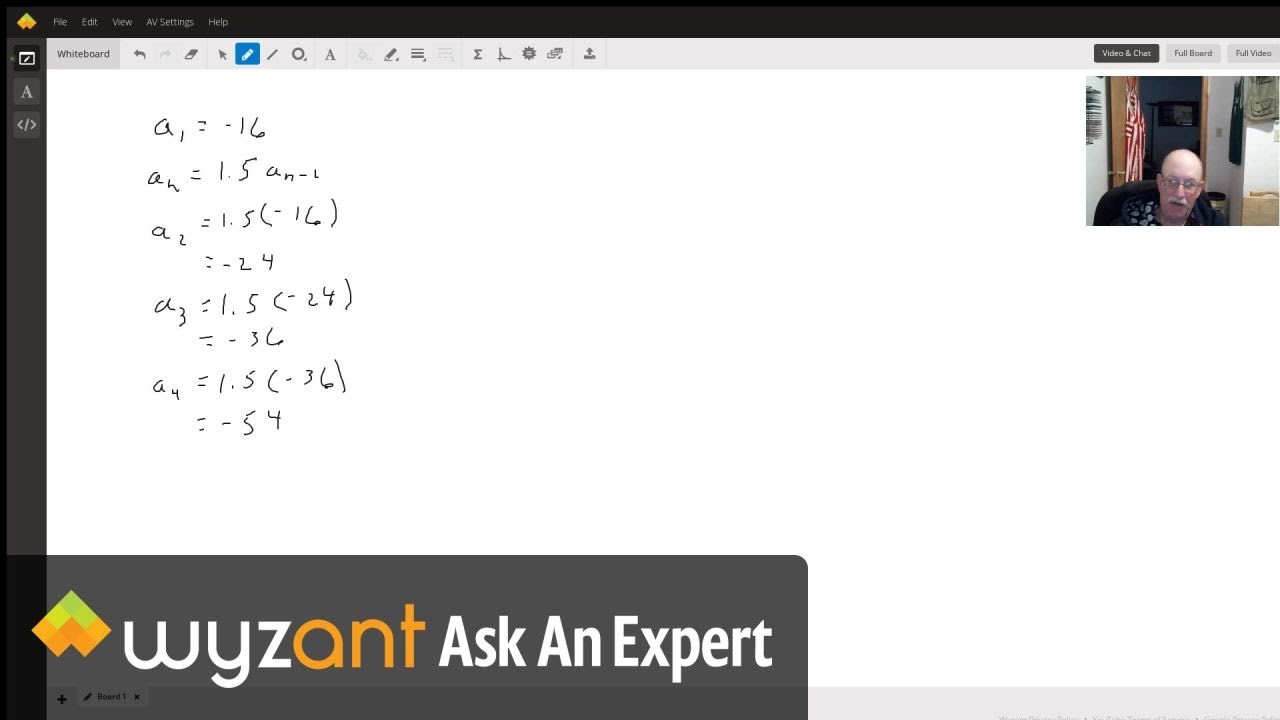
The constant between two consecutive terms is called the common difference.An arithmetic sequence is a sequence where the difference between any two consecutive terms is a constant.Key Equations recursive formula for nth term of an arithmetic sequenceĮxplicit formula for nth term of an arithmetic sequence You can choose any term of the sequence, and add 3 to find the subsequent term.Īccess this online resource for additional instruction and practice with arithmetic sequences. In this case, the constant difference is 3. The sequence below is another example of an arithmetic sequence. For this sequence, the common difference is –3,400. Each term increases or decreases by the same constant value called the common difference of the sequence.

The values of the truck in the example are said to form an arithmetic sequence because they change by a constant amount each year. In this section, we will consider specific kinds of sequences that will allow us to calculate depreciation, such as the truck’s value.

The truck will be worth $21,600 after the first year $18,200 after two years $14,800 after three years $11,400 after four years and $8,000 at the end of five years. The loss in value of the truck will therefore be $17,000, which is $3,400 per year for five years. After five years, she estimates that she will be able to sell the truck for $8,000. One method of calculating depreciation is straight-line depreciation, in which the value of the asset decreases by the same amount each year.Īs an example, consider a woman who starts a small contracting business. This decrease in value is called depreciation. The book-value of these supplies decreases each year for tax purposes.
#Recursive formula for arithmetic sequence definition code#
Recursive functions make the code look clean and elegant.RecursionError: maximum recursion depth exceeded Output Traceback (most recent call last): If the limit is crossed, it results in RecursionError. The Python interpreter limits the depths of recursion to help avoid infinite recursions, resulting in stack overflows.īy default, the maximum depth of recursion is 1000. This is called the base condition.Įvery recursive function must have a base condition that stops the recursion or else the function calls itself infinitely. Our recursion ends when the number reduces to 1. Let's look at an image that shows a step-by-step process of what is going on: This recursive call can be explained in the following steps.ģ * 2 * 1 # return from 3rd call as number=1 When we call this function with a positive integer, it will recursively call itself by decreasing the number.Įach function multiplies the number with the factorial of the number below it until it is equal to one. In the above example, factorial() is a recursive function as it calls itself. Print("The factorial of", num, "is", factorial(num)) Example of a recursive function def factorial(x): Factorial of a number is the product of all the integers from 1 to that number.


 0 kommentar(er)
0 kommentar(er)
